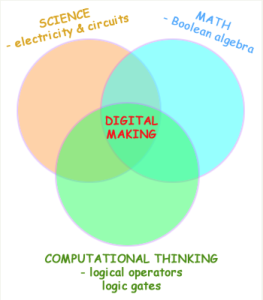
How can digital making take place at the intersection of science, math, and computational thinking?
We start with a look at Venn diagrams, to provide insight into the similarity of the logic involved in each of the following components:
- circuits
- Boolean algebra
- logical operators and gates
Introduction to Venn Diagrams
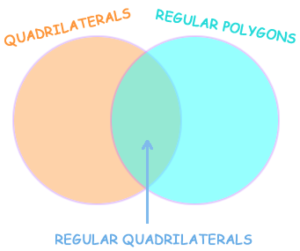
A Venn diagram shows relationships among sets. For example, here are some shapes that belong to the set “quadrilaterals” (i.e., four-sided shapes):

And here are some shapes that belong to the set “regular polygons” (i.e., shapes with equal sides and equal angles):

Which shapes belong to the set of “regular quadrilaterals”? We can represent this visually with a Venn diagram:
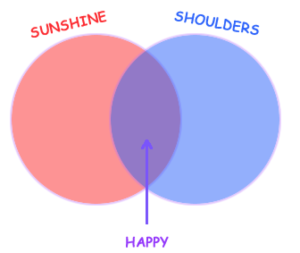
Venn Diagrams with Song Lyrics
In 1971, the singer-songwriter John Denver released the song “Sunshine on my Shoulders”.
The first line of this song is: “Sunshine on my shoulders makes me happy…”
We can represent this as: sunshine AND shoulders = happy
And as a Venn diagram:
Make Your Own Venn Diagram
Use your imagination to create your own Venn diagram relationship:
Connecting Venn Diagrams and Circuits
Let’s build the Venn diagram below with a circuit:
First, fold a piece of cardstock in half (width-wise) and draw the following on the top side.
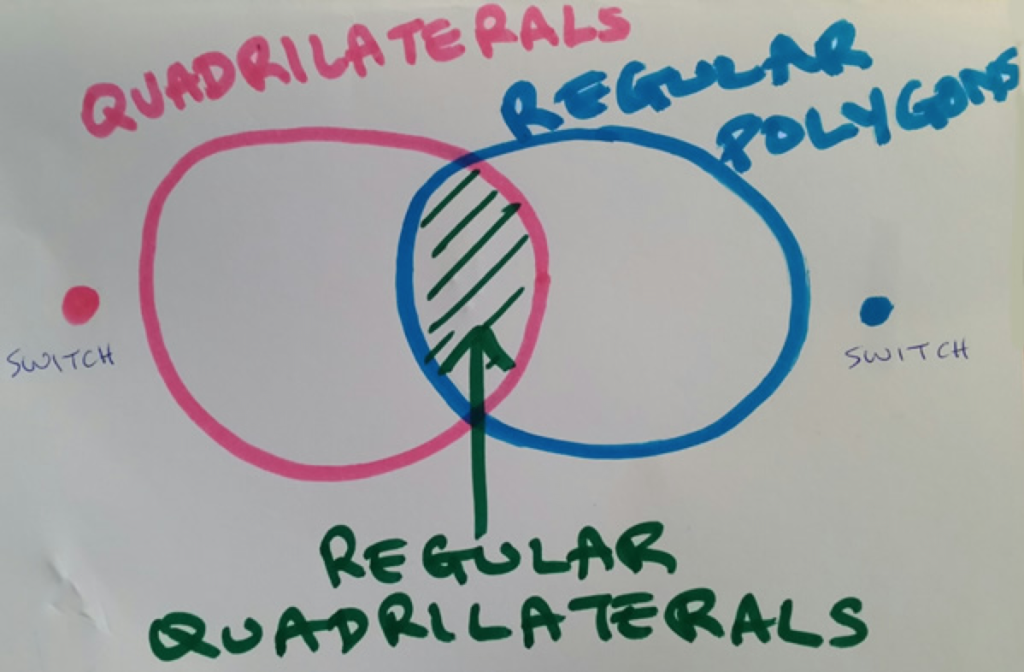 Then, inside the fold, we build this circuit, using: conductive tape, an LED, a 3V battery, and a clip to hold the battery in place.
Then, inside the fold, we build this circuit, using: conductive tape, an LED, a 3V battery, and a clip to hold the battery in place.
 We also add 2 short strips to the underside of the drawing to close the switches when pressed from the other side.
We also add 2 short strips to the underside of the drawing to close the switches when pressed from the other side.
When you close the fold and press on the dots (switches), the LED lights up.
If you close only one OR the other switch, the LED does not turn on. If you close the first switch AND the second switch, the LED turns on.
This circuit is called a SERIES circuit. Notice that all the components are in a single loop, so the current from the battery has only one path to follow.
Connecting Venn Diagrams to Math, Science, and Digital Electronics
Venn diagrams and series circuits connect to mathematics, science and digital electronics.
Mathematics Connection: Boolean Algebra
Sets (like “all the quadrilaterals” or “all the regular polygons”) and their relationships are an important part of math.
Let’s look at sets A and B:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
Here are 3 examples of relationships:
A AND B = {3, 4}
A OR B = {1, 2, 3, 4, 5, 6}
A NOT B = {1, 2}
AND, OR and NOT are 3 examples of how we can create relationships between sets.
Let’s look at two new sets, C and D:
C = {20, 30, 40}
D = {40, 50, 60, 70}}
What would be the resulting sets in each of these relationships?
C AND D = { …………….}
C OR D = { …………….}
C NOT D = { …………….}
All of this is part of the branch of mathematics called Boolean Algebra.
Science Connection: Electricity & Circuits
In science you study electricity and circuits. The series circuit we looked at above is one example. Another example is a parallel circuit, which is shown below.
Notice that closing either switch will complete the circuit, and turn on the LED.
So, in the series circuit, both the first switch AND the second switch must be closed.
And, in the parallel circuit, either the first switch OR the second switch must be closed.
Digital Electronics Connection: Logic Gates
What makes smartphones smart? Smartphones are smart because they can make decisions.
Let’s consider the built-in alarm clock. Suppose you set it for 7 AM.
In order for the alarm to sound:
the clock must be set for 7 AM AND the time must be 7 AM
This decision is made using an AND logic gate, illustrated below.
Boolean Algebra, circuits, and logic gates are different forms of similar ideas.
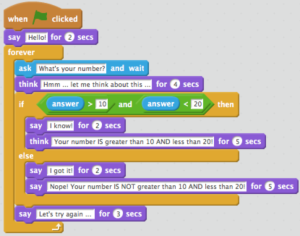
Take it Further: Making Decisions in Scratch (Coding)
Here is Scratch program that decides if the number you enter is greater than 10 AND less than 20.
See and edit the code at scratch.mit.edu/projects/125851999/#editor
Based on ideas discussed in: Hughes, J., Gadanidis, G. and Yiu, C. (2016). Digital making in elementary mathematics education. Digital Experiences in Mathematics Education.
Information for this page was provided by Dr. George Gadanidis.
For more information please refer to George’s website at What will you do in Math today?